La GTO pour les débutants

• 11 juillet 2022
• florian99p99
• 2082
•  PA  0
• 3 Commentaires

On entend souvent parler de la GTO, sans vraiment comprendre ce que signifie ce concept. Dans ce nouvel article, Florian vous présente les bases de la Game Theoty Optimal, et appuiera sa demonstration à travers un exemple concret.

La GTO pour les nuls

Bonjour tout le monde, voici un post qui s’adresse aux personnes débutantes en GTO

On est ici dans la situation la plus simple qui puisse exister au poker, c’est-à-dire dans une situation polarisé vs bluff catcher (PVBC).

Dans ce set up, on dit que le joueur polarisé est clairvoyant sur sa main, c’est-à-dire qu’il sait exactement s’il a la meilleure main ou non, c’est comme si le joueur capped jouait les cartes visibles.

Le joueur qui bluff catch lui est dans le flou total, il ne sait pas si oui ou non il a la meilleure main.
 

C’est deux principes font que le joueur qui bluff catch ne va jamais miser ou relancer, en effet cela n’aurait aucun sens, car si le joueur polarisé a un bluff, il va fold, et s’il a une value, alors il va call (il peut raise avec le bon ratio de bluff, mais restons simple.), ce qui fait que le bet ici n’accomplit rien du tout.
 

Ce principe là fait que ça n’a aucun sens pour le joueur polarisé de slowplay, car le joueur capped ne va jamais bet (en théorie il le peut tant que le slowplay du joueur polarisé ne devient pas > au bet, mais bet n’accomplit rien du tout, donc ignorons cette option).

Ceci fait que la position n’a aucune importance ici, car si le joueur polarisé est OOP, il va check 100 %, et s’il est IP, alors OOP va bet et ça va revenir au même arbre de jeu.


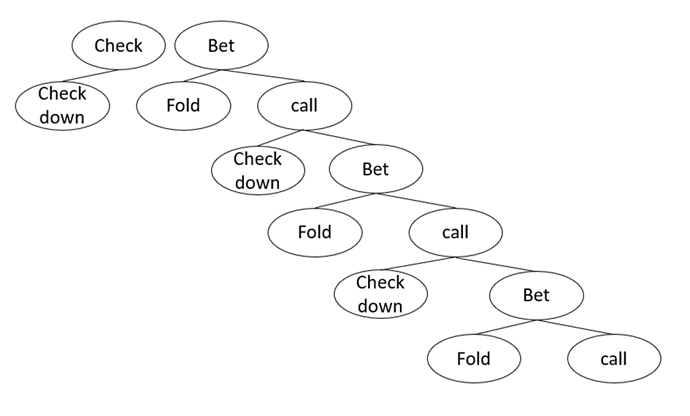
Ceci nous donne donc l’arbre suivant :

 

 

Comment le joueur capped doit défendre ?
 

Malgré la clairvoyance du joueur polarisé sur la force de sa main, le joueur capped va devoir call parfois, et fold d’autre fois, car s’il call 100 % le joueur polarisé ne va jamais bluff, et il va gagner de l’EV avec ces value hands. Et s’il fold 100 %, le joueur polarisé va pouvoir bluff 100 %, et prendre le pot.

Cela crée donc une situation d’indifférence.
 

On a donc l’équation suivante avec les bluffs : EV de bet = EV de check

On a vu plus haut que l’EV de check = zéro, car ça va check down.

Donc 0 = - (Bet) + (pot + Bet) * (Fold)
 

Ce qui nous donne Fold = Bet / (Pot + Bet), le minimum defense frequency (MDF) est donc Pot / (Pot + Bet)

C’est la stratégie du joueur cappé quelques soit la street, il va call Pot / (Pot + Bet), et fold le reste.

Donc sa stratégie va dépendre uniquement du sizing de OOP.

 

Quelle est la stratégie du joueur polarisé ?
 

Le joueur polarisé va vouloir rendre indifférent les calls de vilain. Pour cela il va devoir utiliser le bon ratio de bluff, qui va dépendre uniquement du sizing et du nombre de value hand

Comme le joueur capped est indifférent entre call or fold, cela veut dire qu’au flop nos bluff qui vont 2 barrel vont être considérés comme des value hand
 

Cela fait que l’on doit procéder de façon rétrograde pour trouver le % de bluff au flop :

Par exemple si on a 20 value bet est que l’on bet pot à chaque street

On a pour la river : 
Bet / (Pot + Bet) * (value) = nombre de bluff

0.5 * (20) = 10

Pour la turn
Bet / (Pot + Bet) * (value) = nombre de bluff

0.5 * (30) = 15

Comme nos bluffs river sont considérés comme des value, cela fait que on a 30 value hands.

Pour le flop
Bet / (Pot + Bet) * (value) = nombre de bluff

0.5 * (45) = 22.5

Donc river on va bluff 10 combo, turn 25 combo, et flop 47.5 combo

Donc à la turn on aura une fréquence de bet de 67 % = (20 + 25) / 67.5
 

Remarquez que cela est égal à la côte du pot : En effet, puisque le joueur capped gagne que quand le joueur polar check, cela fait que le joueur polar va devoir check la fréquence de la cote du pot. Cela sera également le cas river.
 

Exemple avec un solver :

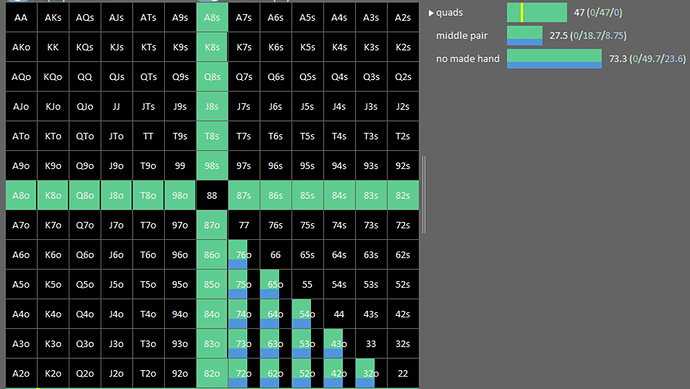
Flop

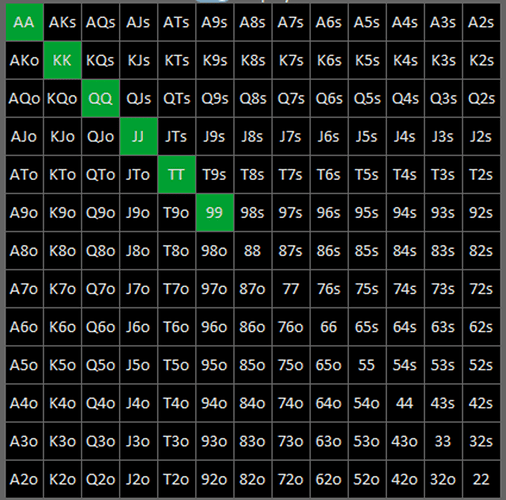
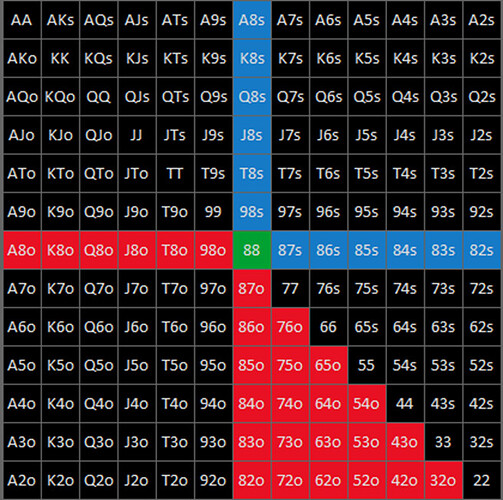
On a les ranges suivante pour OOP et IP

IP pourra bet 50 % du pot au flop, 200 % du pot à la turn, et 100 % river

 

 

 

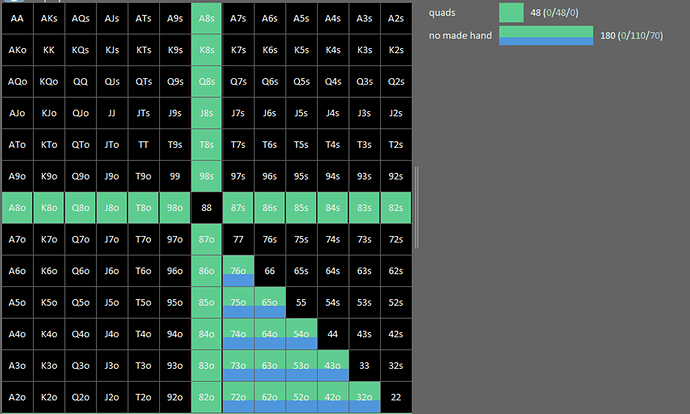
IP a 48 quads, quelle va être le nombre de combo que va bluff IP ?

River

48 * ½ = 24

Turn

72 * 2/3 = 48

Flop

120 * 0.5 / 1.5 = 40

Nombre de bluff flop = 40 + 48 + 24 = 112

 

 

Le solver trouve 110 combos, car il y’a des histoires de blocker de quads sur les turn, mais le but ici c’est de rester simple

Comme au flop on a laissé une cote du pot de 3.2 / 1 cela fait que IP va bet 1 – 1 / 4.2 = 76 %

 

 

 

(Comme il y’a un 8 dans le paquet, j’ai dû exporter les fréquences turn pour le supprimer pour pas polluer les fréquences.)

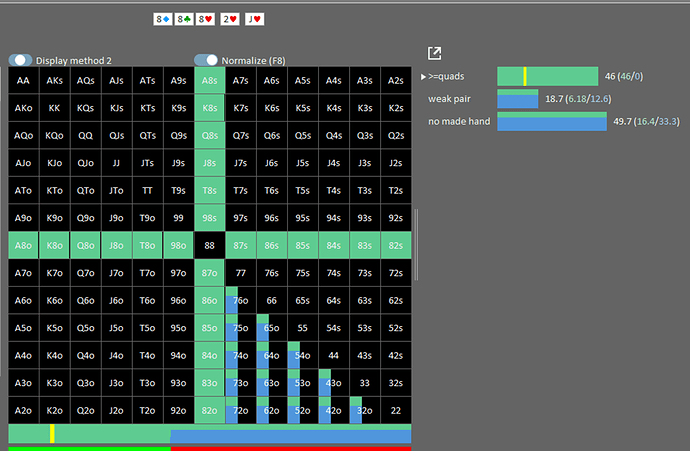
Turn

On a ici plus que 47 quads, car est dorénavant bloqué par le board.

Donc on va bluff un peu moins, soit 68.4 combos

 

 

 

Turn on a laissé à OOP une cote de 1.5 / 1, ce qui fait que river on va bet 1 – 1 / 2.5 = 60 %

Sur un river on a plus que 46 quads, on va donc bluff ½ * 46 = 23

 

 

Conclusion
 

L’EV général de IP pour ce jeu est de 4.48, Il est possible d’augmenter en théorie l’EV de IP, en lui donnant de meilleur sizing (sizing géométrique), cela pourra peut-être faire la suite pour une partie 2.