Le sizing optimal river
De quelle Equity a-t-on besoin pour bet IP ?
Quand on bet vilain va défendre de sorte à rendre notre EV de bluff égale à EV de check.
- Soit : EQ(IP) POT = - BET + freq.fold (BET + POT)
Par exemple si on règle notre équity de bluff sur 0 on a :
- 0 = - BET + freq.fold (BET + POT)
- Freq.fold = BET / (BET + POT)
On peut donc écrire
| Sizing en % pot | MDF | Freq.fold |
|---|---|---|
| 20 | 0,83 | 0,17 |
| 33 | 0,75 | 0,25 |
| 50 | 0,67 | 0,33 |
| 67 | 0,60 | 0,40 |
| 100 | 0,50 | 0,50 |
| 133 | 0,43 | 0,57 |
| 167 | 0,37 | 0,63 |
| 200 | 0,33 | 0,67 |
| 300 | 0,25 | 0,75 |
MDF = minimum defense frequency
On a maintenant une idée de la freq. Fold de vilain face à un bet.
Qu’est-ce que l’équity river ?
River comme il n’existe plus de carte à venir, notre Equity c’est seulement le pourcentage de mains de la range de vilain que l’on domine.
Par exemple si on à 60 % d’équity vs la range de vilain cela veut dire que l’on se fait battre par 40 % de la range de vilain.
Courbe héro en vert :
On voit que héro est devant 60 % des mains, et qu’il est battu par 40 %.
Avec quelles mains peut-on value ?
Nous pouvons écrire l’équation suivante :
- EV check = EV BET
- EQ(IP) POT = -BET + freq.fold (POT + BET) + (1 – freq.fold) (freq de win vs call) (2 BET + POT)
Grace à notre connaissance de l’équity que l’on a vue ci-dessus, on sait que :
- EQ(IP) POT = freq.fold POT + (1 – freq.fold) (freq de win vs call) (POT)
Donc :
- freq.fold POT + (1 – freq.fold) (freq de win vs call) (POT) = -BET + freq.fold (POT + BET) + (1 – freq.fold) (freq de win vs call) (2 BET + POT)
- 0 = -1 + freq.fold + (1 – freq.fold) (freq de win vs call) 2
- 1 – freq fold = (1 – freq.fold) (freq de win vs call) 2
- 1 = (freq de win vs call) 2
- (freq de win vs call) = 1/2
Pour value bet, on doit gagner ½ vs la range call
On peut maintenant connecter toutes nos équations pour obtenir l’équity minimum pour bet x pourcentage du pot
Soit :
- 0.5 = [EQUITY - BET / (BET + POT)] / (POT / (BET + POT)
- EQUITY = 0.5 (POT / (BET + POT) + BET / (BET + POT)]
On peut donc écrire si no air on 0 % d’Equity :
| Sizing en % pot | Equity minimum % |
|---|---|
| 166,00 | 81,20 |
| 133,00 | 78,54 |
| 100,00 | 75,00 |
| 67,00 | 70,06 |
| 50,00 | 66,67 |
| 33,00 | 62,41 |
| 20,00 | 58,33 |
| 10,00 | 54,55 |
| Epsilon | 50 |
Plus nos airs on de l’Equity, plus on devra bet strong.
Exemple solver pour un BET pot (air 0 % Equity):
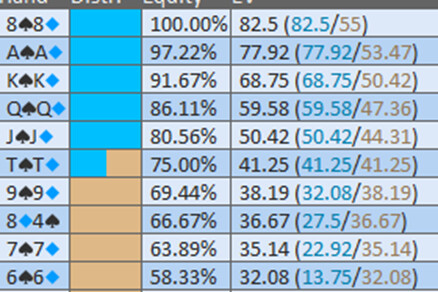
Si on met plusieurs sizes on obtient ceci :
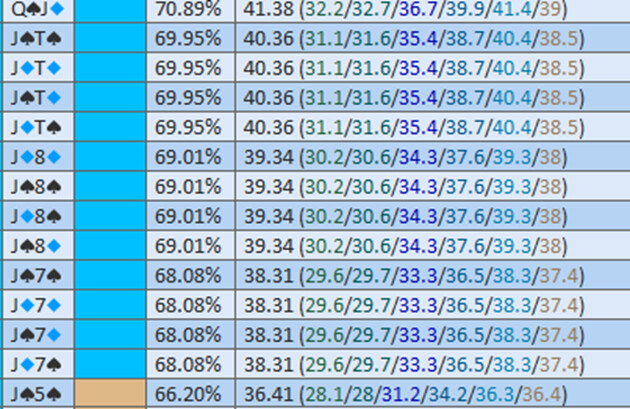
Action solver (pot 100)

Essayons de comprendre pourquoi !
En fait, ce que nous avons trouvé au-dessus c’est l’Equity minimum pour que le bet soit > au check, mais cela ne permet pas de trouver le sizing optimal.
En réalité ce qui se passe, c’est que si nous misons trop cher, on va se faire call plus souvent par mieux, et faire payer plus cher les mains de vilain qui call et que l’on bat.
Si par exemple on bet pot avec une main qui à 75 % d’Equity, on se retrouve juste au seuil de rentabilité. Car on va perdre un BET contre 25 % de la range, gagner 1 BET + POT contre 25 %, et gagner le pot le reste du temps, pour un total EV de 0.75 fois le pot. Soit l’EV que l’on gagne si on check.
Il est possible d’augmenter notre EV en baissant le sizing, car vilain va call plus donc on va gagner plus de value que si on avait simplement check.
Toutefois BET trop small aura pour conséquence que nos value hand vont miss de l’EV, il faut donc trouver le bon compromis.
Comment trouver le sizing optimal.
On peut écrire ceci :
- EV BET = - BET + (freq.fold) (BET + POT) + (1 – freq.fold) (win vs call) (2 BET + POT)
- EV BET = (BET / (POT + BET) + (POT / (POT + BET) – (1 – EQUITY)) (POT + BET) – (1 – EQUITY) (BET)
Remarquons que depuis le début nous n’avons pas pris en compte les raise bluff, mais les équations sont tout à fait en mesure de prendre en compte cette variable, pour cela il faut baisser la fréquence de win vs call, donc down notre Equity, car on va devoir fold contre des bluffs. Vous pouvez remarquer aussi que si vilain utilise une stratégie de raise, mais ne bluff pas, alors c’est exactement la même chose que s’il call. Car dans tous les cas on perd un BET.
On a donc en dérivé 0 :
- Pot / (Pot + BET) ^2 – 2 (1 – EQUITY)
- (1 – EQUITY) 0.5 (POT + BET) ^2
- 0 = 1 – (2) (1 – EQUITY) (1 + 2 (BET) + (BET) ^2)
Avec cette formule on peut maintenant trouver notre sizing optimal.
Reprenons notre exemple de 75 % d’Equity
- 0 = 1 – (2) (1 – 0.75) (1 + 2 (BET) + (BET) ^2)
- 0 = 1 – (0.5) (1 + 2 (BET) + (BET) ^2)
- 0 = 1 – (0.5) - (BET) - 0.5 (BET) ^2)
- 0 = (0.5) - (BET) - 0.5 (BET) ^2)
Ce qui donne :
0.41
Le sizing optimal est 41 % pot size bet
On peut donc écrire :
| Equity | Sizing en pot size bet |
|---|---|
| 66 % | 30 % |
| 75 % | 50 % |
| 82 % | 66 % |
| 87.5 % | 100 % |
| 95 % | 210 % |
Revenons à notre exemple avec le solver
Comme le solver ne peut pas trouver le sizing optimal, on doit donc résoudre 5 équations, et choisir celle qui à le résultat le plus élevé pour trouver le size GTO de l’arbre imposé au solver.
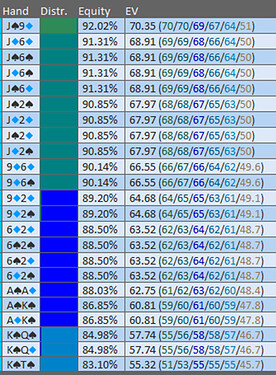
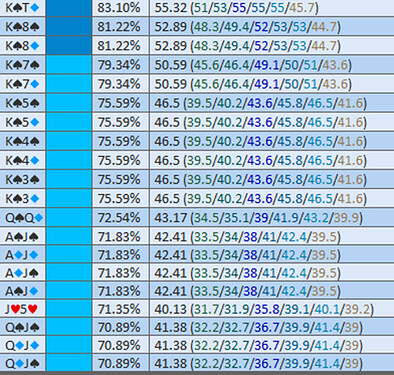
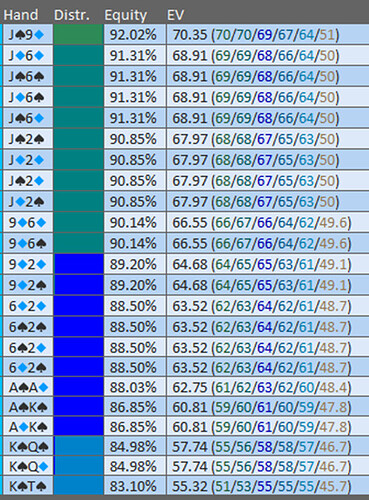
Exemple 9d6s : 90.14 % d’Equity
On va comparer 170, 133, 100, 67, et 50.
- (1.67 / (1 + 1.67)) + (1 / (1 + 1.67) – (1 – 0.9014)) (1 + 1.67) – (1 – 0.9014) (1.67) = 1.19754
- (1.33 / (1 + 1.33)) + (1 / (1 + 1.33) – (1 – 0.9014)) (1 + 1.33) – (1 – 0.9014) (1.33) = 1.20994
- (1 / (1 + 1)) + (1 / (1 + 1) – (1 – 0.9014)) (1 + 1) – (1 – 0.9014) (1.) = 1.2042
- (0.67 / (1 + 0.67)) + (1 / (1 + 0.67) – (1 – 0.9014)) (1 + 0.67) – (1 – 0.9014) (0.67) = 1.17047
- (0.5 / (1 + 0.5)) + (1 / (1 + 0.5) – (1 – 0.9014)) (1 + 0.5) – (1 – 0.9014) (0.5) = 1.13613
Le sizing le plus EV+ des 5, est 133, c’est celui qui est pris par le solver.
Si le solver avait eu le choix entre une infinité de sizing pour cette main, il aurait préféré 1.24:
Sur le même sujet, vous pouvez jeter un œil à l’article d’Alexandre LUNEAU [Blog] Bien choisir son sizing - Le Blog du Team Winamax