Ayant ralenti côté poker dernièrement, je m’intéresse depuis peu au concept de « Massive Open Online Course » (MOOC).
En résumé il s’agit de cours (comme à la FAC) dispensés en ligne gratuitement.
Il en existe sur tous les sujets: science, économie, art etc… J’ai même vu un cours sur l’histoire du Rock et ce n’était pas de la généalogie!
Personnellement je me suis inscrit sur coursera qui d’après ce que j’ai pu tester jusqu’à maintenant, fournit un service de très bonne qualité d’un point de vue pédagogique.
La plupart des cours sont en anglais (on peut télécharger des sous-titres en anglais)
Il se trouve qu’un cours démarre en ce moment sur la théorie des jeux.
Ce cours par des professeurs de l’université de Stanford en Californie dure 9 semaines et demande 7h de travail par semaine.
Il y a un 2ème cours plus avancé prévu.
Chaque cours est composé de videos consultable quand on le souhaite, d’exercices et même d’un examen final.
Je ne sais pas encore si je vais suivre ce cours car j’en suis déjà 2 autres ce qui est ambitieux.
Mais peut être certains seront intéressés.
Je pensais essayer de faire un résumer de chaque video (ce qui me permettrais de m’obliger un bien comprendre les concepts) mais encore une fois je ne suis pas sûr que j’aurai le temps.
Si d’autre son motivés peut-être que je demanderais de l’aide pour se partager le travail.
Sinon je ferais le cours sur plus de 9 semaines à mon rythme.
J’essaierai également d’ajouter mes propres commentaires si j’en ai.
Et chacun pourra commenter bien sûr dans ce thread.
Voici d’ores et déjà un résumé de la 1ère video…
EDIT: J’ajoute le lien vers le cours en question
…Video 1-1 Introduction à la théorie des jeux.
Résumé:
Contrairement à ce que son nom peut laisser entendre la théorie des jeux n’est pas un domaines relatifs aux jeux spécifiquement.
La théorie des jeux est l’étude des stratégies entre participants cherchant chacun à défendre leur propre intérêt.
Pour cette raison la théorie des jeux est importantes dans le domaine économique, politique, informatique, psychologie…
L’intervenant donne un exemple basé sur un problème lié à la technologie des réseaux.
Ce problème peut se résumé ainsi:
2 individus derrière leur ordinateur respectif font face à un message de type popup leur indiquant que s’ils veulent accélérer leur connexion internet il faut qu’il clique Ok (l’alternative étant cancel).
Si les 2 individus préfèrent s’abstenir chacun aura une connexion avec un délais de 1ms
Si un individu clique ok et l’autre cancel alors celui qui clique ok aura un délai de 0ms et l’autre de 4ms
Si les 2 individus cliquent ok alors le délai sera de 3ms pour les 2.
Le but de chacun des participant est de minimiser son délai.
Vis à vis de ce problème il est intéressant de se poser les questions suivantes:
- Quelle action devrait choisir un participant?
- Est-ce que tout le monde ferait le même choix?
- A quel comportement un observateur externe au jeu peut-il s’attendre?
- Que se passe-t-il si l’on change les valeurs des délais?
- Que se passe-t-il si les 2 participants peuvent communiquer?
- Que se passe-t-il si le problème est répété n fois entre les participants?
- Est-ce que le fait que je vois mon adversaire comme quelqu’un de rationnel est important?
Mes commentaires
On retrouve avec ce première exemple et dans les questions soulevées certaines problématiques liés au poker.
En particulier sur l’importance des sizing, côte du pot (question 4), la stratégie à long terme (question 5), et l’adaptation au profil adverse (questions 2 & 7).
…Video 1-2 Agents avec intérêts personnels et fonction d’utilité
La théorie des jeux fait intervenir les 2 concepts d’Agent avec intérêt personnel (self-interested Agents) et la fonction d’utilité.
Les self interested Agent représente les participants (en général un individu) aux « jeux » (au sens large) considéré. Chaque agent a sa propre perception de la valeur d’une situation donnée dans le jeu.
Cette valeur est mesurée par ce qu’on appelle la fonction d’utilité (utility function) de l’agent.
Suivant le type de « jeu » considéré, les « self-interested Agents » ne sont pas nécessairement adversaires. Par exemple un agent peut inclure dans son estimation de la valeur d’une situation donnée le bien-être d’autres agents.
Dans la théorie des jeux on suppose que chaque agent prend des décisions qui optimisent la valeur de sa propre fonction d’utilité. D’autre part on suppose que la valeur de la fonction utile est représentée par un nombre unique (dit autrement une valeur unidimensionnelle).
Ces 2 hypothèses ne sont pas triviales. Par exemple si on prend le cas de la fonction d’utilité d’un individu qui donnerait la valeur du bien-être de celui-ci en fonction de sa santé et de sa richesse il n’est pas évident qu’il soit réaliste de mettre ces 2 paramètres sur un même axe.
De même il n’est pas évident qu’un individu prenne toujours une décision qui va améliorer son bien être et donc optimiser la valeur de sa fonction d’utilité.
Mes commentaires
[i]
Si l’on fait l’analogie avec le poker on pourrait dire que les « self-interested agents » sont les joueurs et la fonction d’utilité est la fonction qui donne l’EV en fonction du move.
Mais en prenant cette définition on se place dans un contexte théorique GTO (ce qui est peut être un peu le but de la théorie des jeu).
Dans la pratique personne ne connait la fonction qui donne l’EV en fonction du move (sinon cela voudrait dire que le poker est résolu), et par ailleurs même si c’était le cas un joueur peu choisir d’autres options que le move optimal en EV.
- Parce qu’il considère que d’autre paramètre que maximiser l’EV est important par ex. limiter la variance.
- Parce qu’il est en tilt et/ou a envie de gambler.
Ces 2 cas semblent assez différents a priori.
Dans le premier cela signifie juste que la fonction d’utilité de ce joueur n’est pas la fonction qui maximise l’EV.
Dans le 2ème cas il s’agit d’une réponse émotionnelle qu’il est plus délicat d’intégrer dans la fonction d’utilité à moins de voir ça comme une façon de se défouler: Le joueur retire plus de bénéfice à gambler parce que cela lui permet de faire passer sa frustration même s’il perd de l’EV.
[/i]
…Video 1-3 Définir un « jeu »
Listons les éléments qui permettent de définir et modéliser un « jeu »:
- Les joueurs: Ceux qui prennent des décisions. Suivant le type de jeu il peut s’agir d’individus ou de gouvernements, d’entreprise, etc…
- Les actions: Ce que chaque joueur peut faire. Faire une enchère, décider ou non de faire grève, miser au poker.
- La rétribution: Ce qui motive chaque joueur. Argent, bien-être, etc…
En théorie des jeux il existe 2 type de représentation d’un jeu:
- La forme normale pour laquelle tous les joueurs agissent de façon simultanée
- La forme extensive qui inclue la notion de temps. Chaque joueur joue en séquence comme aux échecs ou au poker.
Dans cette video on s’intéresse à la première forme.
Une représentation d’un jeu sous la forme normale est modélisée ainsi:
- L’ensemble des joueurs est noté: N={1,…,n} n joueurs indexé par i
- L’ensemble des actions possibles du joueur i est noté Ai
…- a=(a1,…,an) est un profil d’action. Cela correspond à un ensemble d’action, 1 par
…joueur. Par exemple dans le jeu de la première video, (Ok,Cancel) est un profil
…d’action signifiant que le joueur 1 à cliqué sur ok et le joueur 2 sur Cancel. - La fonction d’utilité du joueur i noté ui.
…- u=(u1,u2,…,un) est un profil de fonction utile.
En forme normal un jeu avec 2 joueurs peut être représenté sous forme d’une matrice m x n (ou tableau) avec
- m le nombre d’actions possibles pour le joueur 1
- n le nombre d’actions possibles pour le joueur 2
Chaque case du tableau indique le gain (c’est à dire le résultat de la fonction utile en fonction de l’action de chaque joueur)
Si l’on prend l’exemple du jeu de la video 1 la matrice est une matrice 2 x 2 (chaque joueur peut faire 2 actions, cliquer sur ok ou sur cancel):
[center]
[/center]
C et D correspondent respectivements aux actions « clique sur ok » et « clique sur cancel ».
Le premier nombre de chaque case indique le gain (ici le délai) pour le joueur 1 et le 2ème nombre le gain pour le joueur 2.
Ansi la première case (case C,C) nous indique que si les 2 joueurs « cliques sur ok » alors ils ont chacun un délai de 1ms.
Si joueur 1 clique sur ok et joueur 2 clique sur cancel (case C,D) alors le joueur un a un délai de 4ms et le joueur 2 de 0ms.
Cette représentation sous forme d’une matrice m x n n’est pas possible pour un grand nombre de joueur.
Il faut alors utiliser une autre représentation plus formelle.
Supposons par exemple un jeu avec un grand nombre de joueurs qui sont les citoyens d’un pays totalitaire de 10 million d’habitants N={1,…,10 000 000)
Chacun a le choix entre se révolter et ne pas se révolter.
La fonction utile de chaque citoyen pourrait être définie ainsi:
- ui(a) = 1 quel que soit l’action du citoyen i si au moins 2 000 000 de citoyens se révoltent (ils sont assez nombreux pour que la révolte soit un succès et bien qu’il n’est pas participé le citoyen i va profiter de la sortie de l’état totalitaire.)
- ui(a) = -1 si le citoyen i se révolte et que moins de 2 000 000 de citoyens se révoltent (la révolte est un échec et les révoltés seront punis)
- ui(a) = 0 si le citoyen ne se révolte pas et que moins de 2 000 000 de citoyens se révoltent. Pour le citoyen i rien ne change.
Mes commentaires
[i]
La représentation normale n’est pas applicable au poker puisque chaque joueur agit à tour de rôle.
On pourrait envisager une variante du poker ou les joueurs jouent de façon simultanée :-).
Par exemple le joueur qui mise le plus remporte le coup et en cas de mise égale c’est celui qui a le jeu le plus fort qui gagne.
Comme exercice vous pouvez essayer de faire la matrice correspondante en supposant que tout se passe à la rivière avec un pot de 10BB et que chaque joueur peut soit miser 0,5BB,10BB, 20BB :-)…
Voila ma matrice. Je ne peux pas affirmer à 100% qu’elle est correcte.
BH= Best hand (meilleure main)
WH = Worst hand (moins bonne main)
Certaines cases sont grisées car ce n’est pas possible que les 2 joueurs aient la meilleure main (ou la moins bonne).
Je néglige les cas de split.
[/i]
…Video 1-4 Exemples de jeux
Résumé:
Cette video donne quelques exemples de jeux.
D’abord des jeux de pure compétition: Les joueurs ont des intérêts exactements opposés.
Cela se traduit, en utilisant les concepts/notations précédents par la formule:
Quelque soit le profil d’action a de A, u1(a) + u2(a) = c avec c une constante.
Cela signifie que ce qui est gagné par un joueur est perdu par l’autre.
En particulier si c = 0 on a un jeu à somme nulle (comme au poker).
par exemple: Chaque joueur choisit entre pile et face si les 2 joueurs choisissent la même face alors le joueur 1 gagne 1€ et l’autre perd 1€ sinon c’est le contraire.
Un autre exemple est pierre papier ciseau.
Un autre type de jeu est le jeu de pure coopération lorsque les joueurs ont le même intérêt.
La définition formelle de ce type de jeux est:
Quelque soit a appartenant à A, quelque soit i,j, ui(a) = uj(a)
Cela signifie que tous les joueurs ont la même fonction d’utilité.
Par exemple: 2 piétons marchent l’une vers l’autre sur le trottoirs risquant de se percuter.
Chacun doit choisir entre se détourner vers la droite ou vers la gauche.
Si les 2 font le même choix les 2 piétons gagnent
Sinon les 2 perdent.
…Video 1-5 Equilibre de Nash Intro
Résumé:
L’équilibre de Nash est un des concepts de base de la théorie des Jeux.
John Nash est un mathématicien de Princeton a gagné un prix Nobel pour ces travaux sur le domaine.
Pour introduire ce concept imaginons que nous possédons des actions en bourse dont le prix a atteint un niveau qui vous semble élevé.
Vous pensez qu’il est temps de les vendre mais vous souhaitez les vendre au plus haut.
Pour cela il faut que vous vous demandiez comment les autres acheteurs/vendeurs voient cette action et qu’elle va être leur stratégie.
Ce la représente la base de l’équilibre de Nash. Vous ne devez pas baser votre stratégie sur ce que vous pensez (ici le fait que l’action est cher) mais sur ce que vous pensez que les autres pensent.
Pour étudier l’équilibre de Nash nous allons, dans les prochaines video utiliser le jeu suivant:
Vous être N joueur.
Chaque joueur choisit un entier entre 1 et 100.
Celui qui se rapproche le plus de 2 tiers de la moyenne des nombres choisis a gagné.
En cas d’égalité un tirage au sort est effectué pour déterminer le gagnant.
…Video 1-6 Raisonnement Strategique
La stratégie qui permet d’atteindre l’équilibre de Nash est la suivante:
- Quel choix vont faire les autres joueurs
- Quel est la réponse la plus adaptée
- Chaque joueur sélectionne la meilleur réponse vis à vis des choix des autres joueurs.
Tentons de faire le raisonnement sur le jeu présenté à la video précédente.
Les joueurs ne peuvent pas choisir un nombre supérieur à 100 donc le maximum de la moyenne est 100.
2/3 * 100=67.
Donc, si un joueur réfléchit correctement il ne devrait pas dire un nombre supérieur à 67.
Donc si tous les joueurs réfléchissent correctement la moyenne est au plus de 67.
Donc, si un joueur réfléchit correctement il ne devrait pas dire un nombre supérieur à 2/3 * 67
Et en poursuivant le raisonnement on arrive à un équilibre de Nash où tous les joueurs répondent 1.
Voici les résultats du jeu sur un échantillons de 10000 joueurs:
[center]
[/center]
On constate que les joueurs n’ont pas jouer Nash.
Certains ont jouer une valeur supérieure à 67
On a un pic à 50.
On a également un pic à 33 qui montre que certains avaient anticipé que pas mal de joueurs joueraient 50 (33=2/3=50)
On a également un pique vers 23 qui est environ 2/3 de 33 donc certains joueurs ont anticipé que pas mal de joueurs allaient anticicper que pas mal de joueurs joueraient 50.
Enfin on a un pic proche de 0 qui correspond à ceux qui ont compris Nash et décider de suivre cette stratégie.
Le vainqueur a finalement joué 23.
On fait ensuite une 2ème partie avec les mêmes joueurs:
[center]
[/center]
On constate que les joueurs ont largement corriger le tir pour se rapprocher de 0 et donc de Nash.
En résumé l’équilibre de Nash consiste en une stratégie ou chaque joueur maximise ses gains en fonction des actions des autres, aboutissant à un profile d’action stable où aucun joueur n’a intérêt de dévier de sa stratégie.
…Video 1-7 Meilleure réponse et équilibre de Nash
Notons a-i=<a1,…ai-1,ai+1,…an> : Il s’agit d’un profile d’action auquel on a retiré l’action du joueur i.
Le profil d’action complet est donc ai=(a-i,ai).
a-i est donc la stratégie auquel le joueur i fait face de la part de tous les autres participants.
La meilleure réponse pour a-i est définie ainsi:
[center]
[/center]
Cette formule doit être lu ainsi ai* est une meilleure réponse contre le profil d’action partiel a-i si et seulement si quelque soit une autre action ai du joueur, le gain obtenu par la stratégie ai* est supérieure ou égal au gain obtenu en choisissant la stratégie ai.
L’équilibre de Nash est alors défini ainsi:
[center]
[/center]
C’est à dire qu’un équilibre de Nash est un profil d’action tel que chaque action est une meilleur réponse vis à vis des stratégies des autres joueurs.
La notion de « pure strategy » sera expliquée plus tard dans le cours.
…Video 1-8 Examples d’équilibres de nash
L’équilibre de Nash s’obtient donc lorsqu’aucun participant n’a intérêt à changer de stratégie connaissant la stratégie des autres joueurs.
Voici quelques exemples d’équilibre de Nash:
Le dilemme du prisonnier bien connu est représentée par la matrice suivante:
Si les 2 prisonniers se dénoncent mutuellement ils prennent 3 ans de prison.
S’ils se taise ils prennent 1 an.
Mais si l’un parle et l’autre se tait alors celui qui parle est libre et l’autre prend 4ans.
Si les 2 prisonniers pouvaient négocier entre eux ils choisiraient sans doute la 2ème option.
Mais sachant que les 2 prisonniers sont séparés et ne connaissent pas le choix de l’autre le seul équilibre de Nash est de parler.
Il peut y avoir plusieurs équilibres de Nash.
Par exemple dans le jeu ou 2 personnes marchent l’une vers l’autre et doivent choisir de tourner à droite ou à gauche pour s’éviter il y a 2 équilibres de Nash qui consiste à ce que les 2 participants choisissent le même côté pour ne pas se rentrer dedans.
Il peut également ne pas y avoir d’équilibre de Nash.
Chaque participant choisit pile ou face. Si les 2 joueurs choisissent la même chose c’est le joueur 1 qui gagne sinon c’est le joueur 2.
La meilleure réponse à pile est donc face pour le joueur 2.
Mais si le joueur 2 choisit face alors le joueur 1 à intérêt à choisir face également.
Du coup le joueur 1 doit prendre pile.
Et ainsi de suite…
On arrive jamais à une situation d’équilibre dans laquelle aucun des joueurs n’a intérêt à changer de stratégie connaissant la stratégie adverse.
…Video 1-9 Stratégie dominantes
Définition:
Un stratégie si domine strictement une stratégie s’i si quelque soit la stratégie des autres joueurs, le joueur i obtient un meilleur gain avec la stratégie si.
Un stratégie si domine faiblement une stratégie s’i si quelque soit la stratégie des autres joueurs, le joueur i obtient un gain au moins aussi bon avec la stratégie si.
Cela peut être mis sous la forme suivante:
[center]
[/center]
Si une stratégie domine tous les autres stratégies alors on dit qu’elle est dominante.
Si une telle stratégie existe alors le joueur doit l’appliquer quel que soit la stratégie des autres joueurs.
Un profil d’action qui ne contient que des stratégies dominante pour chaque joueur est un équilibre de Nash. Si les stratégies sont strictement dominantes alors il n’existe qu’un seul équilibre de Nash.
Dans le dilemme du prisonnier quel que soit la stratégie du joueur 1 le joueur 2 obtient toujours un meilleur gain en choisissant la stratégie consistant à parler.
Donc la stratégie « parler » est une stratégie strictement dominante.
La même chose s’applique au joueur 1.
On a donc un équilibre de Nash qui consiste en 2 stratégies strictement dominantes.
…Video 1-10 Pareto optimum
Définition:
Un profil d’action o1 pareto-domine un profil d’action o2 si pour chaque joueur o1 offre un gain au moins égal à o2 et si pour certains joueurs o1 offre un gain strictement supérieur à o2.
Un profil d’action qui n’est pareto-dominer par aucun profil d’action est un optimum de Pareto.
[u]
Remarques:
Un jeu peut avoir plusieurs optimum de Pareto.
Un jeu a toujours au moins un optimum de Pareto.
Exemples:[/u]
- Dans le jeu ou chaque joueur marche l’un vers l’autre vu précédemment, il y a 2 optimum de Pareto:
[center]
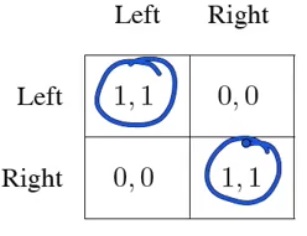[/center]
- Dans le jeu de pile ou face tous les profils d’action sont des optimum de Pareto:
- Dans le jeu du dilemme du prisonnier tous les profils d’action sont des optimum de Pareto sauf 1
Le profil (-3,-3) n’est pas un optimum de Pareto parce qu’il est pareto-dominé par le profil (-1,-1).
On voit dans le cas du dilemme du prisonnier que la seule solution qui ne soit pas un optimum de Pareto est la solution correspondant à un équilibre de Nash.
