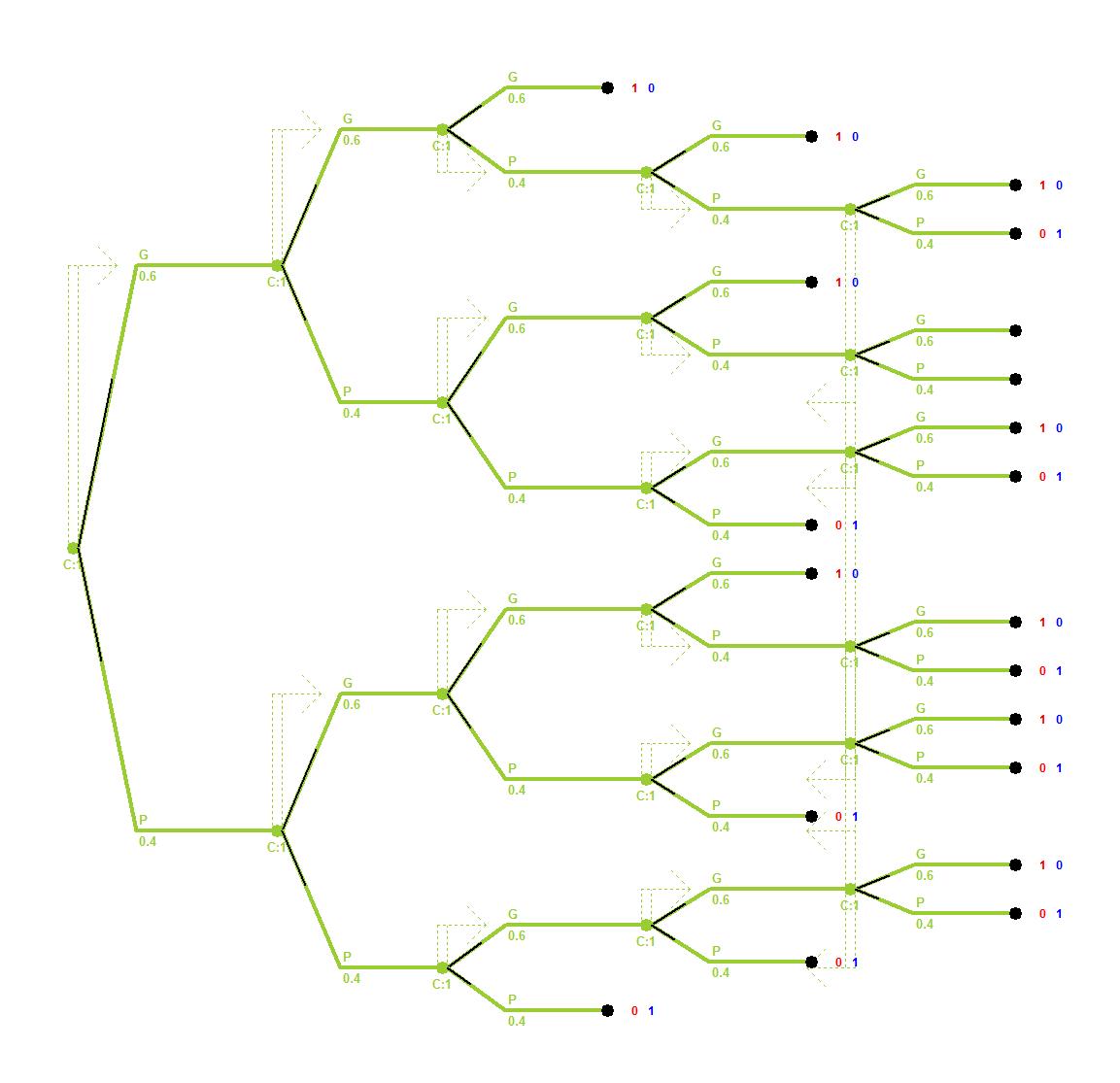
[quote=“Benjamin_Shal, post:803082”][quote=“Yeepaa, post:803079”][quote=“TheDeus72, post:803063”]En fait c’est une loi binomiale :

On a k le nombre de succès, n le nombre de parties (5 ou 7), p la probabilité de succès (60%) et q la probabilité d’échec (40%)
Du coup pour un BO5 on a besoin de gagner 3 matchs ou plus donc il faut calculer P(X=3), P(X=4) et P(X=5)
Pour un BO7 il faut calculer P(X=4), P(X=5), P(X=6) et P(X=7)
En gros pour gagner un BO5 avec une proba de gagner chaque match de 60% on a :
P(X=3) = (20/2) * (0,6)^3 * (0,4)^2 = 0,35
P(X=4) = (5) * (0,6)^4 * 0,4 = 0,26
P(X=5) = 1 * (0,6)^5 * 1 = 0,08
On additionne les probas ensuite, avec les arrondis ca fait : 0,68256
Pour un BO7 avec les mêmes formules (sauf qu’on prends n=7) et qu’on calcule P(X=4), P(X=5), P(X=6) et P(X=7) on obtient 0,71021[/quote]
plop
huge TY
j’ai essayé d’expliquer à Benj
[13:01:07] Yeepaa - Manuel Antunes -: c’ets la loi binomiale
mais ce poulpe était en mode

 :S :evil: :evil: :silly: :silly: :blink: :blink:
:S :evil: :evil: :silly: :silly: :blink: :blink:
°+°[/quote]
T’es sérieux là ? Tu veux que je sorte la discussion ?
Parce que TheDeus est quand même BEAUCOUP plus clair dans ces explications. Limpide même.
Merci à toi !
PS : j’aime bcp ce magazine sinon[/quote]
plop
hahahaha
bah de 1 : loin de moi l’idée de croire que tu pouvais envisager de commencer à comprendre ce genre de chose => 
de 2 : fallait bien que je réussisse à parler de ton magazine préféré  (on peut reparler du brésil si tu veux
(on peut reparler du brésil si tu veux  :D)
:D)
de 3 : faut bien que je te fasse chier pendant qu’on t’a encore sous la main 


de 4 : je me suis évertué à te faire comprendre/faire dire (parce que pète boules comme t’es tu l’avais très bien comprit !) pourquoi ce n’était pas ton résultat qui m’importait mais la démarche globale et si tu veux on reparle du "il y a que le résultat qui compte "
de 5 : ça me fait tellement rire de parler avec toi 


°+°